下面是小编为大家整理的数学典故，希望大家能够从中有所收获!

1958年美国的《心理学杂志》上，彭罗斯发表了他的不可解的三接棍。如图1-1。他称之为立体的矩形构造：三个直角并显示出垂直，但它是不可能存在于空间的，因为在这里三个直角似乎成了一个“三角形”，但三角形是平面而非立体的图形，三个内角和为180°，而非270°。

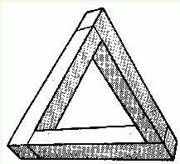
图1-1

图1-2

20世纪50年代，罗格和彭罗斯写了论不可能图形的文章，文章描述了一种“没有尽头的楼梯”，踏着楼梯好像是一步一步地上升，然而楼梯都是停留在一个水平面上。如图1-2。

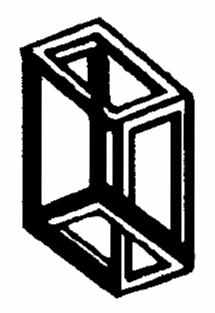
图1-3

荷兰著名画家埃舍尔被认为是20世纪公认的视错觉画大师。他的作品以其深刻的数学、物理含义特别得到科学家的重视。如图1-3，他为第十届国际数学大会(1981年奥地利)所作的会标，就是一个三维空间不可能的图形。