反三角函数是一种数学术语。反三角函数并不能狭义的理解为三角函数的反函数，是个多值函数。它是反正弦Arcsin x，反余弦Arccos x，反正切Arctan x，反余切Arccot x这些函数的统称，各自表示其正弦、余弦、正切、余切为x的角。以下是小编为大家整理的关于反三角函数定义域，欢迎大家前来阅读!

反三角函数定义域

y=arcsin(x)，定义域[-1，1]

y=arccos(x)，定义域[-1，1]

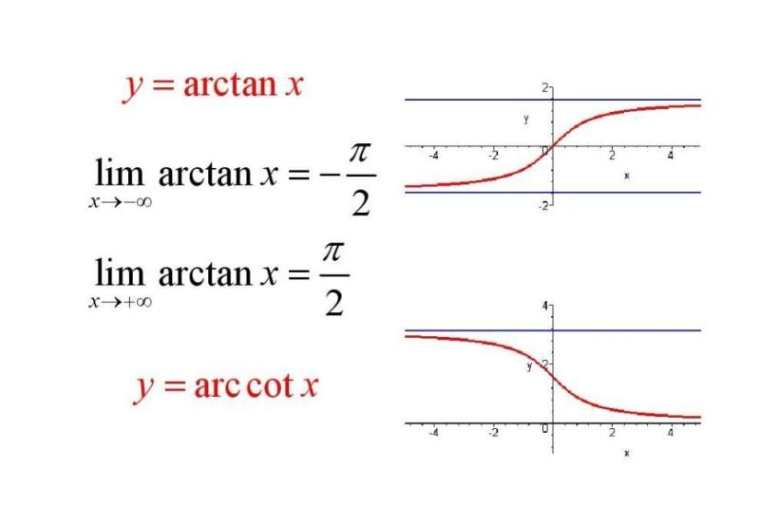
y=arctan(x)，定义域(-∞，+∞)

y=arccot(x)，定义域(-∞，+∞)

sin(arcsin x)=x，定义域[-1，1]

反三角函数数学术语

为限制反三角函数为单值函数，将反正弦函数的值y限在-π/2≤y≤π/2，将y作为反正弦函数的主值，记为y=arcsin x;相应地，反余弦函数y=arccos x的主值限在0≤y≤π;反正切函数y=arctan x的主值限在-π/2

反三角函数实际上并不能叫做函数，因为它并不满足一个自变量对应一个函数值的要求，其图像与其原函数关于函数y=x对称。其概念首先由欧拉提出，并且首先使用了【arc+函数名】的形式表示反三角函数，而不是f-1(x)。

⑴正弦函数y=sinx在[-π/2，π/2]上的反函数，叫做反正弦函数。arcsinx表示一个正弦值为x的角，该角的范围在[-π/2，π/2]区间内。【图中红线】

⑵余弦函数y=cosx在[0，π]上的反函数，叫做反余弦函数。arccosx表示一个余弦值为x的角，该角的范围在[0，π]区间内。【图中蓝线】

⑶正切函数y=tanx在(-π/2，π/2)上的反函数，叫做反正切函数。arctanx表示一个正切值为x的角，该角的范围在(-π/2，π/2)区间内。【图中绿线】

注释：【图的画法根据反函数的性质即：反函数图像关于y=x对称】

反三角函数主要是三个：

y=arcsin(x)，定义域[-1，1]，值域[-π/2，π/2]图象用深红色线条;

y=arccos(x)，定义域[-1，1]，值域[0，π]，图象用深蓝色线条;

y=arctan(x)，定义域(-∞，+∞)，值域(-π/2，π/2)，图象用浅绿色线条;

y=arccot(x)，定义域(-∞，+∞)，值域(0，π)，暂无图象;

sin(arcsinx)=x，定义域[-1，1]，值域[-1，1]arcsin(-x)=-arcsinx

证明方法如下：设arcsin(x)=y，则sin(y)=x，将这两个式子代入上式即可得

其他几个用类似方法可得

cos(arccosx)=x，arccos(-x)=π-arccosx

tan(arctanx)=x，arctan(-x)=-arctanx

反三角函数数学公式

反三角函数其他公式：

cos(arcsinx)=(1-x^2)^0.5

arcsin(-x)=-arcsinx

arccos(-x)=π-arccosx

arctan(-x)=-arctanx

arccot(-x)=π-arccotx

arcsinx+arccosx=π/2=arctanx+arccotx

sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x

arcsinx=x+x^3/(2*3)+(1*3)x^5/(2*4*5)+1*3*5(x^7)/(2*4*6*7)……+(2k+1)!!*x^(2k-1)/(2k!!*(2k+1))+……(|x|<1)!!表示双阶乘

arccosx=π-(x+x^3/(2*3)+(1*3)x^5/(2*4*5)+1*3*5(x^7)/(2*4*6*7)……)(|x|<1)

arctanx=x-x^3/3+x^5/5-……

举例

当x∈[-π/2，π/2]有arcsin(sinx)=x

x∈[0，π]，arccos(cosx)=x

x∈(-π/2，π/2)，arctan(tanx)=x

x∈(0，π)，arccot(cotx)=x

x>0，arctanx=π/2-arctan1/x，arccotx类似

若(arctanx+arctany)∈(-π/2，π/2)，则arctanx+arctany=arctan((x+y)/(1-xy))

例如，arcsinχ表示角α，满足α∈[-π/2，π/2]且sinα=χ;arccos(-4/5)表示角β，满足β∈[0，π]且cosβ=-4/5;arctan2表示角φ，满足φ∈(-π/2，π/2)且tanφ=2