在考试快要到来的时候，我们作为学生应该做出什么样的复习准备工作呢?下面请欣赏网络编辑为你带来的华师大版八年级上 14.2勾股定理的应用练习卷，希望你能够喜欢!

华师大版八年级上 14.2勾股定理的应用练习卷

选择题

(2014•钦州)如图，在6个边长为1的小正方形及其部分对角线构成的图形中，如图从A点到B点只能沿图中的线段走，那么从A点到B点的最短距离的走法共有( )

A．1种

B．2种

C．3种

D．4种

(2013•济南)如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8m处，发现此时绳子末端距离地面2m，则旗杆的高度为(滑轮上方的部分忽略不计)为( )

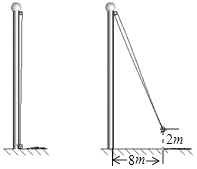
A．12m

B．13m

C．16m

D．17m

(2013•余姚市模拟)已知：如图，无盖无底的正方体纸盒ABCD﹣EFGH，P，Q分别为棱FB，GC上的点，且FP=2PB，GQ=QC，若将这个正方体纸盒沿折线AP﹣PQ﹣QH裁剪并展开，得到的平面图形是( )

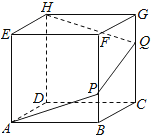
A．一个六边形

B．一个平行四边形

C．两个直角三角形

D．一个直角三角形和一个直角梯形

(2013•沙坪坝区模拟)如图，AC是电杆的一根拉线，测得BC=6米，∠ACB=60°，则AB的长为( )

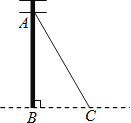
A．12米

B．米

C．6米

D．米

(2013•镇江模拟)已知圆锥的母线长OA=8，底面圆的半径为2，一小虫在圆锥底面的点A处绕圆锥侧面一周又回到点A处，则小虫所走的最短距离为( )

A．8

B．4π

C．8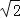

D．8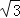

(2012•黄冈模拟)将边长分别为3cm，3cm，2cm的等腰三角形从一个圆钢圈中穿过，那么这个圆钢圈的最小直径是( )cm.

A．2

B．2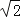

C．3

D．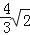

(2012•乐山市中区模拟)一船向东航行，上午8时到达B处，看到有一灯塔在它的南偏东60°，距离为72海里的A处，上午10时到达C处，看到灯塔在它的正南方向，则这艘船航行的速度为( )

A．18海里/小时

B．海里/小时

C．36海里/小时

D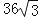．海里/小时

(2012•平谷区二模)如图是一个长方体，AB=3，BC=5，AF=6，要在长方体上系一根绳子连接AG，绳子与DE交于点P，当所用绳子的长最短时，AP的长为( )

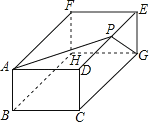
A．10

B．

C．8

D．

(2011•金华)如图，西安路与南京路平行，并且与八一街垂直，曙光路与环城路垂直.如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程约为( )

A．600m

B．500m

C．400m

D．300m

(2013•鄂州)如图，已知直线a∥b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB=.试在直线a上找一点M，在直线b上找一点N，满足MN⊥a且AM+MN+NB的长度和最短，则此时AM+NB=( )

A．6

B．8

C．10

D．12

(2014•邯郸二模)如图，圆柱底面半径为

cm，高为9cm，点A、B分别是圆柱两底面圆周上的点，且A、B在同一母线上，用一根棉线从A点顺着圆柱侧面绕3圈到B点，则这根棉线的长度最短为( )

A.12cm B.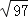

cm C.15cm D.cm

(2014•荆州)如图，已知圆柱底面的周长为4dm，圆柱高为2dm，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为( )

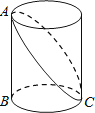
A．4dm

B．2dm

C．2dm

D．4dm

(2014•龙东地区)一圆锥体形状的水晶饰品，母线长是10cm，底面圆的直径是5cm，点A为圆锥底面圆周上一点，从A点开始绕圆锥侧面缠一圈彩带回到A点，则彩带最少用多少厘米(接口处重合部分忽略不计)( )

A．10πcm

B．10cm

C．5πcm

D．5cm

(2014•中山模拟)如图，一个梯子AB长2.5米，顶端A靠在墙AC上，这时梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测得BD长为0.9米，则梯子顶端A下落了( )

A．0.9米

B．1.3米

C．1.5米

D．2米

(2014•北塘区二模)有甲、乙两块铁板(厚度忽略不计)，甲的形状为直角梯形，两底边长分别为4cm，10cm，且有一内角为60°;乙的形状为等腰三角形，其顶角为45°，腰长12cm.在不改变形状的前提下，试图分别把它们从一个直径为8.7cm的圆洞中穿过，结果是( )

A．甲板能穿过，乙板不能穿过

B．甲板不能穿过，乙板能穿过

C．甲、乙两板都能穿过

D．甲、乙两板都不能穿过

(2014•平谷区一模)在某次活动课中，甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息：如图1，甲组测得一根直立于平地，长为80cm的竹竿的影长为60cm.如图2，乙组测得学校旗杆的影长为900cm.则旗杆的长为( )

A．900cm

B．1000cm

C．1100cm

D．1200cm

(2014•博山区模拟)如图，点A的正方体左侧面的中心，点B是正方体的一个顶点，正方体的棱长为2，一蚂蚁从点A沿其表面爬到点B的最短路程是( )

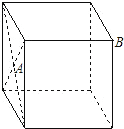
A．3

B．

C．

D．4

(2014•石家庄二模)如图，若圆柱的底面周长是30cm，高是40cm，从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处做装饰，则这条丝线的最小长度是( )

A．80cm

B．70cm

C．60cm

D．50cm

(2013•安顺)如图，有两颗树，一颗高10米，另一颗高4米，两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢，问小鸟至少飞行( )

A．8米

B．10米

C．12米

D．14米

(2011•台湾)已知小龙、阿虎两人均在同一地点，若小龙向北直走160公尺，再向东直走80公尺后，可到神仙百货，则阿虎向西直走多少公尺后，他与神仙百货的距离为340公尺?( )

A．100

B．180

C．220

D．260