下面是小编为大家整理的数学典故，带你探索数学的图形世界，希望大家能够从中有所收获!

如果让你考虑一个这样的问题：“具有有限面积的平面图形，其周长是有限的，还是无限的呢?”你会毫不犹豫地说：“当然周长也是有限的。”

在我们现在学习的几何中，人们总是用诸如点、线、平面、三角形、正方形、圆这样的对象和概念来描述我们生存的这个世界。然而1906年瑞典数学家科克作了一条“雪花曲线”，它的面积是有限的，然而它的周长是无限的。

雪花曲线的具体做法是这样的。先作一个等边三角形(如图1)，再把每边三等分，将居中的1/3部分向外作一个小等边三角形，并把每一个小等边三角形的底抹掉，得到一个六角星形(如图2));再在六角星形的每一条边上以同样的方法向外作出更小的等边三角形，于是曲线变得越来越长，开始像一片雪花了(如图3))。再如此作下去，曲线将变得越来越长，图形也更美丽(如图4)。如果不断地作下去，则曲线可以要多长有多长，若无限地如此作下去，自然就有无限周长了。而这个图形的面积，通过计算，最多只能是原来三角形的8/5倍。

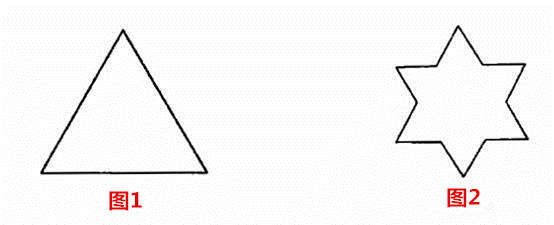
意大利数学家欧内斯托·切萨罗曾对科克雪花曲线作过如下描述：这个曲线最使我们注意的地方是任何部分都与整体相似。这个结构的每一个小三角形包含着一个适当比例缩小的整体形状。这个形状包含着每一小三角形的缩小形式，后者又包含缩得更小的整体形状，如此下去以致无穷。就是这个在它所有的无论怎样小的部分都保持着相似的性质，使这曲线看上去是如此的奇妙。要是它在现实中出现，那就必须把它完全除去才能摧毁它。否则的话，它将会从它的三角形的深处重新不停地生长起来，就像宇宙本身一样。